Decision Trees in Machine Learning

Decision Trees in Machine Learning

How can a machine classify any given dataset?

One way to build a classification model is using decision trees. Decision trees break down the dataset into smaller parts which represent calculated decision. Each decision has its resulting nodes which can be either decision or leaf node. Decision node has at least two branches. Whereas a leaf node has only one decision which is end-decision. Decision trees start with one node called root node.

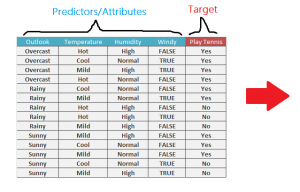
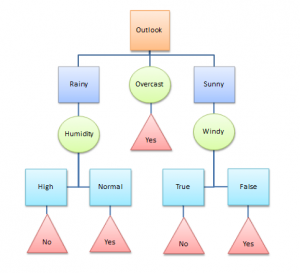
Algorithm Behind Decision Trees

The most important algorithm in creating decision trees is called ID3 created by J. R. Quinlan. ID3 algorithm breaks dataset into a top-down list. Using Information Gain and Entropy functions to decide on whether adding a predictor/attribute into a decision or not. For instance, new branches of decision will be created if entropy of attribute leading the decision is the highest information gain.

Entropy

ID3 algorithm uses entropy function to calculate how similar different subsets of the data. If selected set of data is leading the same result in each case (completely homogeneous), then entropy is zero. If the sample of data is equally divided in terms of results, then entropy is one.

a) Calculating entropy with one attribute’s frequency table:



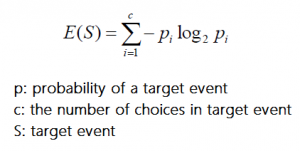
b) Calculating entropy with tow attribute’s frequency table:

Information Gain

Information gain from an attribute is the decrease in entropy when the dataset is splitted by the attribute. Apparently, it tells you which attribute splits the data into more homogeneous branches. Building a decision tree come downs to finding the attribute returning the highest information gain.

Gain (T, X) = Entropy (T) – Entropy (T,X)

Gain(Play Tennis, Outlook) = Entropy(Play Tennis) – Entropy(Play Tennis, Outlook)

= 0.94 – 0.693 = 0.247

Steps of ID3 algorithm:

1. Select a root Node

In order to build a decision tree, there needs to be a root node which is the best attribute/predictor to be selected which gives the most valuable information.

2. Calculate the information gained for each attribute

Entropy for each attribute should be calculated then it will be subracted from the total entropy to find the information gained (decrease in entropy).

3. Choose the decision node: Attribute with the highest information gain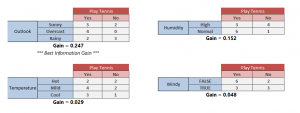



4. Calculate entropy for each branch of the decision node. Determine whether given branch is leaf node or not.

Leaf node is a decision that always lead to the same expected condition. It has entropy value of zero.



 

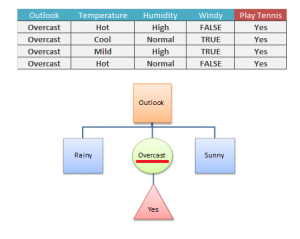5. Branch nodes with non zero entropy needs to be splitted further

6. Recursively follow steps 2 through 5 to classify (split) the remaining data   

Things to Consider when Building Decision Trees:

• Not working good with non-homogenous branches


• Some attributes may have small number of values which can be skipped


• Dataset may be overfitted and resulting with errors